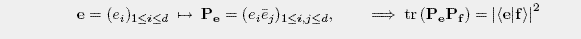MUBs (Mutually Unbiased Bases) and SIC POVMs
(Symmetric Informationally Complete Positive Operator Valued Measures) are both regular
quantum designs with r=1. Such designs are also called spherical designs,
as they can be described using normalized vektors e
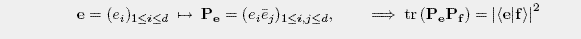
- MUBs
are regular (r=1) and affine quantum designs. In the vector description
the orthogonal classes are orthogonal bases, were for vectors e, f from different bases
one gets |<e|f>|2=1/d.
The maximum number of MUBs is d+1. Sets of d+1 MUBs when d is a prime
were first found by I.D.Ivanovic (1981). W.K.Wooters and B.D.Fields established 1989 the term "mutually unbiased"
and gave solutions of d+1 MUBs whenever d is a power of a prime.
In my master thesis (1991) this
concept was independently rediscovered and generalized to irregular designs
(independent observables, see next page).
Furthermore maximal solutions were found the for more general concept of affine quantum designs with
r(d2-1)/(d-r) complete orthogonal classes
whenever d is a powers of a prime.
For d=6 an infinite family of MUB-triples was constructed and it was (probably the first time)
conjectured that 4 MUBs don't exist in this dimension.
For an overview see T.Durt, B.G.Englert, I.Bengtsson, K.Zyczkowski
arXiv:1004.3348 (external link).
- SIC POVMs
are regular (r=1) quantum designs with degree 1 and d2 elements.
For any two different vectors e, f the equation <e|f>|2=1/(d+1) holds. Thus
the vectors span d2 equiangular lines.
Equiangular lines were first investigated by J.J.Seidel (1966, 1973, ...) et.al., mainly for the real case.
S.G.Hoggar (1982) analyzed the complex case and gave solutions (of d2 vectors) for
d=2,3 and 8.
In my Ph.D. thesis (1999) further maximal analytic and numerical
solutions weren given and it was (probably the first time) conjectured that such
solutions in the complex case exist in any dimension d (generated by the Weyl-Heisenberg group
and with a certain additional symmetry of order 3).
J.M.Renes, R.Blume-Kohout, A.J.Scott and C.M.Caves independently analyzed the same structures in 2003,
gave further numerical solutions and coined
the term SIC-POVM.
The most recent and advanced paper on this topic is by Marcus Appleby, Steven T. Flammia, and Gene S. Kopp
arXiv:2501.03970 (external link).
It can be shown, that both, sets of d+1 MUBs (more generally affine quantum designs with
r(d2-1)/(d-r) complete orthogonal classes) and SIC-POVMs (more generally regular
quantum designs with degree 1 and d2 elements) are
quantum 2-design with respect to the group G = U(d), of all unitary matrices.
|
| Dieser Text ist nur auf Englisch verfügbar |
|