-
Quantendesigns: Grundzüge einer nichtkommutativen Designtheorie,
Ph.D. Thesis, University of Vienna, 1999
-
Download (German, pdf, 77 pages, 442 KB).
-
Quantum Designs: Foundations of a non-commutative Design Theory,
English translation of the Ph.D. Thesis (including a new preface 2010)
-
Download (pdf, 79 pages, 468 KB).
Published in the International Journal of Quantum Information (IJQI), Volume 9, Issue 1, February 2011, page 445-507.
[DOI No: 10.1142/S0219749911006776], © Copyright World Scientific Publishing Company,
see IJQI.
The thesis contains an overall presentation of quantum designs, based on the terminology
given here.
A list of Citations (external link).
-
Orthogonale Lateinische Quadrate und Anordnungen, Verallgemeinerte Hadamard-Matrizen und
Unabhängigkeit in der Quanten-Wahrscheinlichkeitstheorie,
Master (Diploma) Thesis, University of Vienna, 1991 -
Download (German, pdf, 87 pages, 7273 KB)
This paper contains a presentation and analysis of the concept of independent observables -
a generalization of affine designs. The spectral decomposition

of k self-adjoint matrices A1, ..., Ak defines k
complete orthogonal classes on the quantum design built up from all the projections. The orthogonal
classes, resp. obervables, Ai are said to be mutually independent
(w.r.t. the density matrix (1/d)I), if

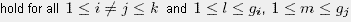 . .
For regular quantum design this reduced to the definition of affine designs, and with the case r=1
to MUBs. This definition also covers the (basic) mutually independence of
Ai = Bi 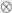 I and
Aj = I I and
Aj = I 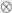 Bj for any
selfadjoint matrices Bi, Bj. Bj for any
selfadjoint matrices Bi, Bj.
This definition also allows a generalization to infinite dimensional Hilbert Spaces: Let A
and B be two self-adjoint operators over a seperable Hilbert-Space with spectrum
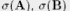 respectively. Let further respectively. Let further 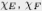 be the characteristic
functions of Borel subsets E, F of the spectrum of A and B, hence be the characteristic
functions of Borel subsets E, F of the spectrum of A and B, hence
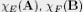 be spectral projections of A and B. be spectral projections of A and B.
We say that A and B are independent if there are Borel
measures 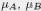 on the spectrum of A and B such,
that for any two compact subset
E and F the following relation holds: on the spectrum of A and B such,
that for any two compact subset
E and F the following relation holds:

Please notice, that for arbitrary projections P1 and P2
in infinite-dimensional Hilbert spaces
tr(P1P2P1) =
tr(P2P1P2) holds (the expression
tr(P1P2) is generally not defined).
It can be shown, that the position operator X
and the impuls operator P are mutually independent, as well as linear-combinations of these two.
|
| Dieser Text ist nur auf Englisch verfügbar |
|